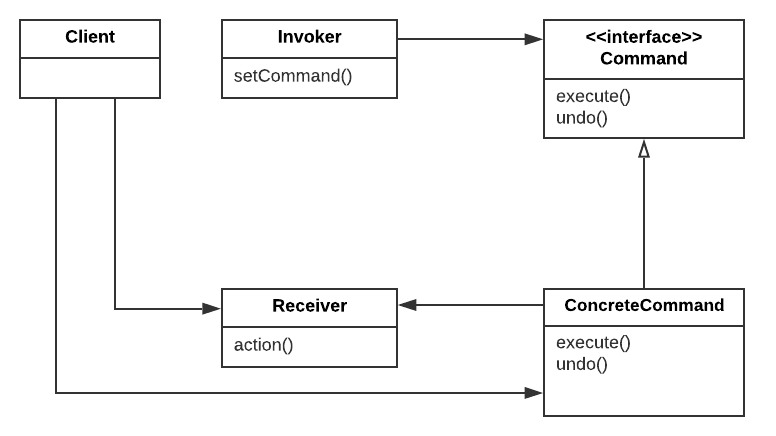
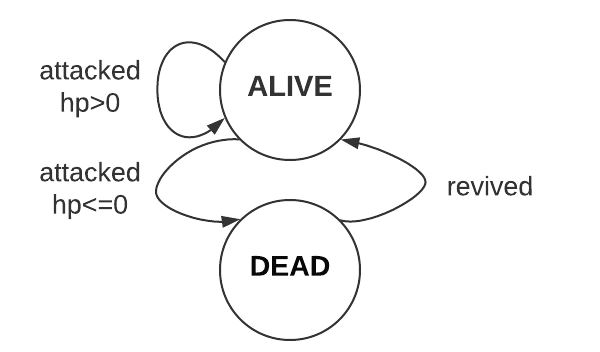
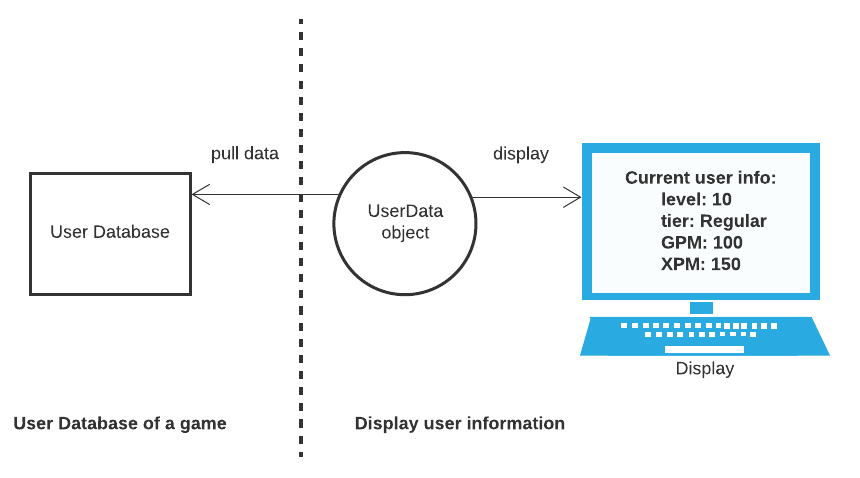
This March, I got promoted to a senior machine learning engineer. Stepping into this new role, I thought I was more than prepared. After all, people only get promoted to the next level after they already function like the next level. Now, I have worked as a senior engineer for half a year, and I gradually realize that while the daily technical work may appear similar for a senior engineer, being a senior engineer opens many doors and prompts me to think what I truly want for my career.