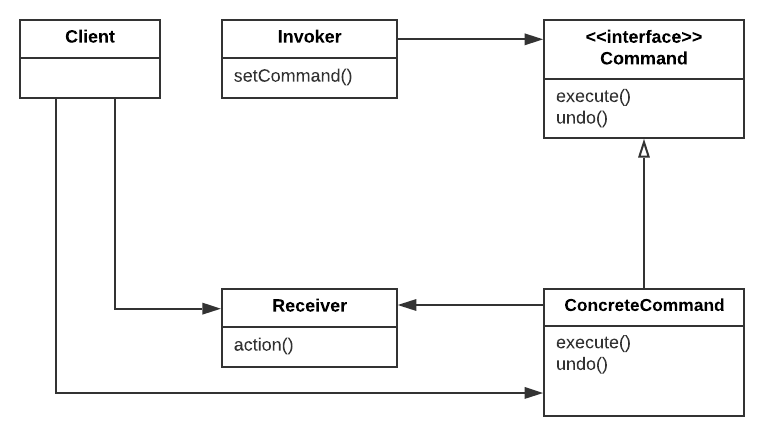
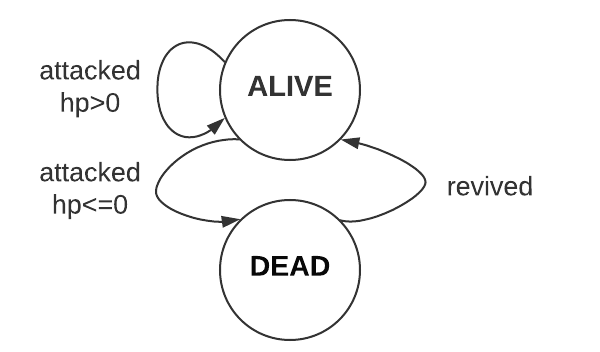
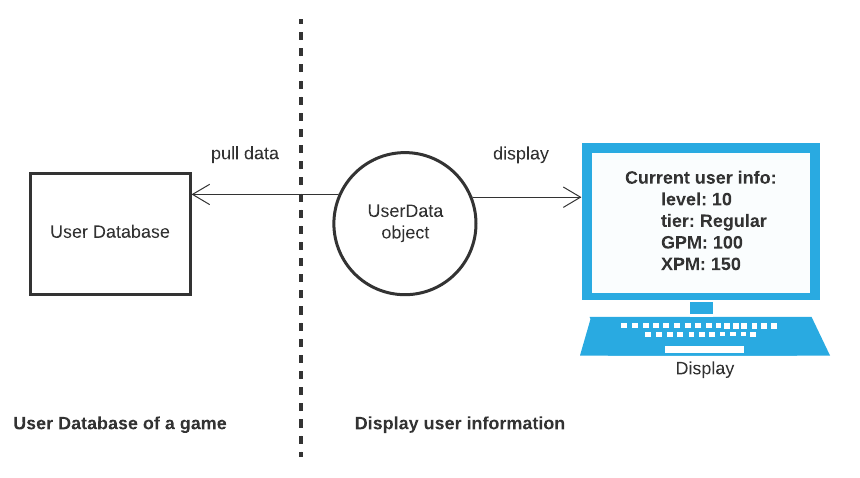
This March, I got promoted to a senior machine learning engineer. Stepping into this new role, I thought I was more than prepared. After all, people only get promoted to the next level after they already function like the next level. Now, I have worked as a senior engineer for half a year, and I gradually realize that while the daily technical work may appear similar for a senior engineer, being a senior engineer opens many doors and prompts me to think what I truly want for my career.
After more than a year of working from home, my husband and I took a 2-week trip to Hawaii to celebrate our 2nd anniversary. The trip was like a dream, and we both fell in love with nature and the vibe of Hawaii. In this post, I will share our itinerary and recommendations for traveling in Hawaii.
In this post, I will talk about how to ensure only 1 instance of a class is created using the Singleton pattern.
See code at Github repo (https://github.com/yangju2011/design-patterns). Code is adapted from Head First Design Patterns: A Brain-Friendly Guide 1st Edition by Eric Freeman and Elisabeth Robson.
In this post, I will use the Command Pattern to order a burger and manage a job queue. Command pattern encapsulates a request (method invocation) as an object, and parameterizes and schedules requests.
In this post, I will use the State Pattern to alter the behaviors of a hero when it is under attack or being silenced. State pattern allow us to encapsulate states into separate classes and delegate behaviors to the object representing the current state.
In this post, I will use the observer pattern and pub/sub pattern to build a game user display to show user’s information.
In this post, I will introduce the strategy pattern and factory patterns using Dota2 Heroes as examples. Dota2 is a multiplayer online battle arena (MOBA) video game, a sequel to Defense of the Ancients (DotA), played in matches between two teams of 5 players. Each player independently controls a powerful character, known as a “hero”, with unique abilities and roles.
In the past few months, I have been learning software design patterns and reading the book Head First Design Patterns: A Brain-Friendly Guide 1st Edition by Eric Freeman and Elisabeth Robson. Here I’d like to share what I’ve learned.