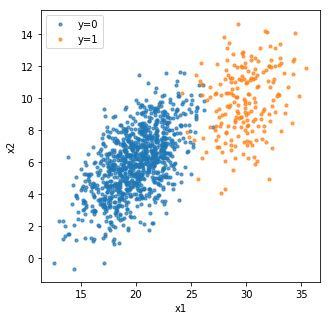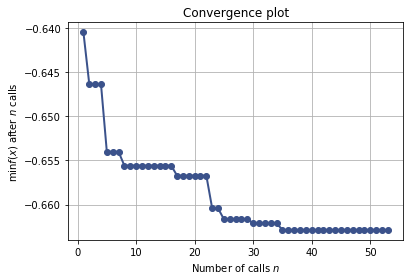
In machine learning models, we often need to manually set various hyperparameters such as the number of trees in random forest and learning rate in neural network. In traditional optimization problems, we can rely on gradient-based approaches to compute optimum. However, hyperparameter tuning is a black box problem and we usually do not have an expression for the objective function and we do not know its gradient. In this post, I will discuss different approaches for hyperparameter tuning and how we can learn to learn.