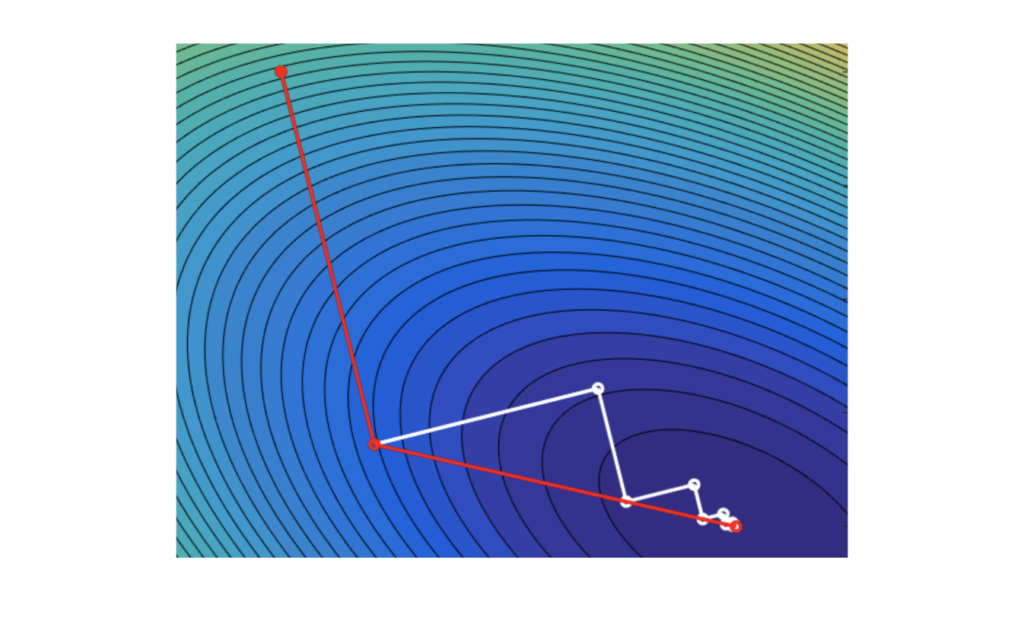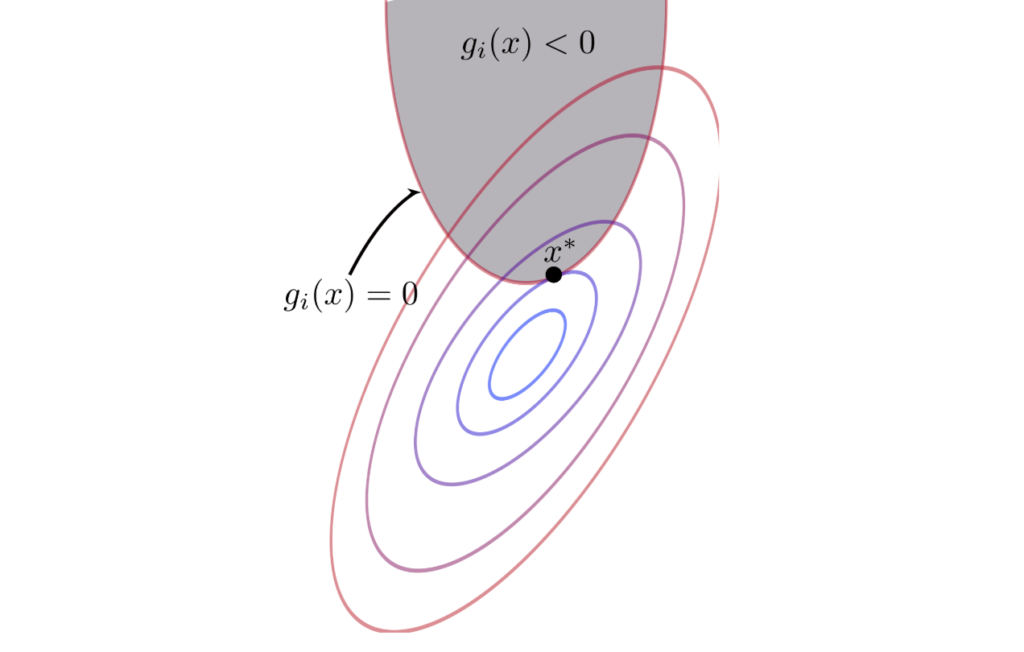
Now what we have discussed unconstrained optimization problems in previous post, it is now time to come to the reality. In the real world, we often have limitations, such as the total budget, motion angles, and some arbitrary desirable range of values. Life would be so easy (and boring) without boundary and conditions. Adding constraints certainly makes optimization problems less easy, but more interesting.
Why do we care about eigenvalues, eigenvectors, and singular values? Intuitively, what do they tell us about a matrix? When I first studied eigenvalues in college, I regarded it as yet another theoretical math trick that is hardly applicable to my life. Once I passed the final exam, I shelved all my eigen-knowledge to a corner in my memory. Years have passed, and I gradually realize the importance and brilliance of eigenvalues, particularly in the realm of machine learning. In this post, I will discuss how and why we perform eigendecomposition and singular value decomposition in machine learning.
