In the previous post, I talked about using MapReduce and Spark for distributed model training. In this post, I will talk about parameter server and how it is used in distributed model training.
Posts in the Connect the Dots category:
Distributed model training I: MapReduce and Spark
In the previous post, I introduced challenges in machine learning systems with big data and complex models. In this post, I will discuss distributed systems in the era of big data.
Think big: ML systems in the era of big data
Let’s start with linear regression. Using established libraries such as scikit-learn, it is almost trivial to train a linear regression model. We can easily run the model training with a few hundred Megabytes of data on our laptop with a build-in CPU.
Now let’s think big.
Machine Learning Lifecycle
In business management, product lifecycle is broken into 4 stages with the distinct pattern of sales over time: introduction, growth, mature, and decline. In the diagram below, I adapt the classic product lifecycle curve to show the engineering load over time in machine learning (ML): from model development to maintenance. Managing and coordinating different stages in ML lifecycle presents pressing challenges for ML practitioners.
5 things you need to know about Machine Learning Systems
The more I work on building end-to-end machine learning (ML) pipelines, the more I realize the importance of system design and infrastructure. ML shares many concerns with traditional software development, and poses new challenges to system design.
Reinforcement learning (II): Markov Decision Process and RL agent
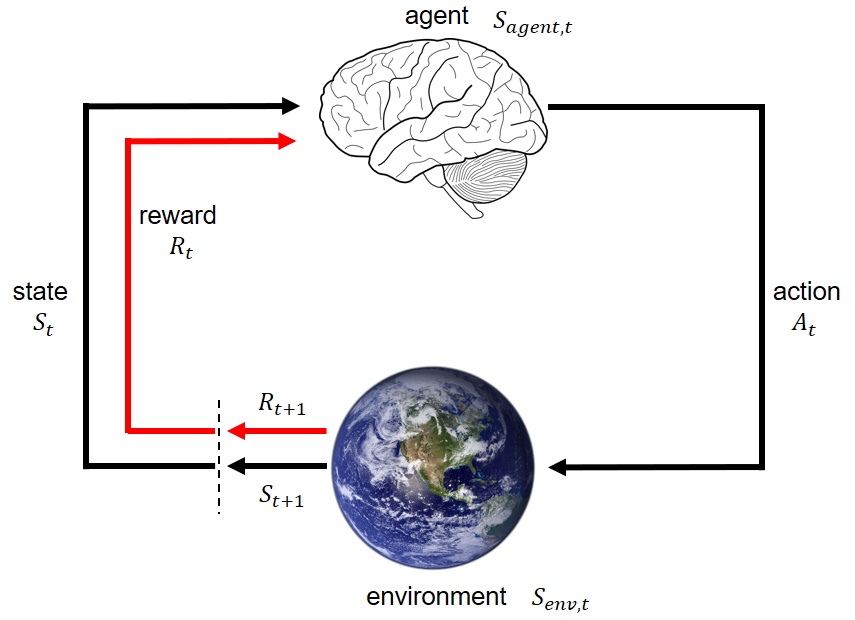In the previous post,I gave a high-level overview of Reinforcement Learning (RL). In this post, I will summarize different learning paradigms of RL agents. (more…)
Reinforcement learning (I): overview
In the past 2 years, I have been following progress in Reinforcement Learning (RL). RL beats human experts in Go [1], and achieves professional levels in Dota2 [2] and StarCraft [3]. RL is being mentioned more and more often in mainstream media and conferences.
I think it is a good time for me to revisit RL. (more…)
How exactly does Bayesian Optimization work?
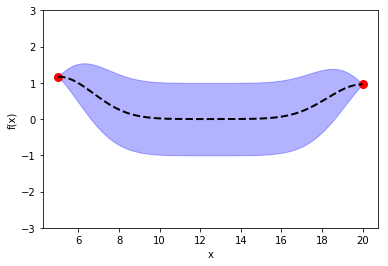
In the previous post, I introduced Bayesian Optimization for black-box function optimization such as hyperparameter tuning. It is now time to look under the hood and understand how the magic happens.