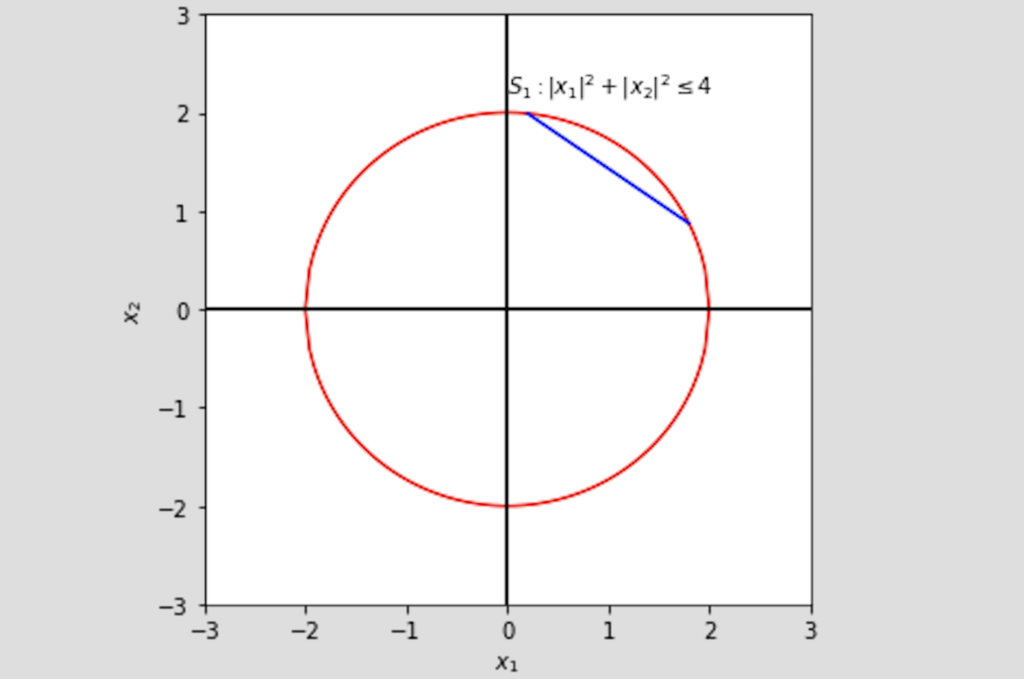
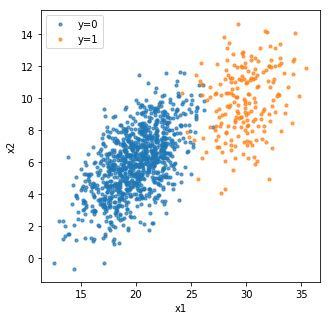
In machine learning, we are often dealing with high-dimension data. For convenience, we often use matrix to represent data. Numerical optimization in machine learning often involves matrix transformation and computation. To make matrix computation more efficiently, we always factorize a matrix into several special matrices such as triangular matrices and orthogonal matrices. In this post, I will review essential concepts of matrix used in machine learning.
During logistic regression, in order to compute the optimal parameters in the model, we have to use an iterative numerical optimization approach (Newton method or Gradient descent method, instead of a simple analytical approach). Numerical optimization is a crucial mathematical concept in machine learning and function fitting, and it is deeply integrated in model training, regularization, support vector machine, neural network, and so on. In the next few posts, I will summarize key concepts and approaches in numerical optimization, and its application in machine learning.
Last February, I defended my PhD thesis and graduated from more than 2 decades of school life. Now, it’s been a full year of post-school life. There are no more exams and curriculum to quantify my GPA. In this post-school life, I start to realize that I have to be the one setting my own goal, designing my own curriculum, and evaluating my progress introspectively. In this post, I am sharing some lessons that I find useful in DIY curriculum.
In the previous post, I have discussed loss function in regression. In this post, I will elaborate how we develop loss function in classification when the output is discrete, rather than continuous.