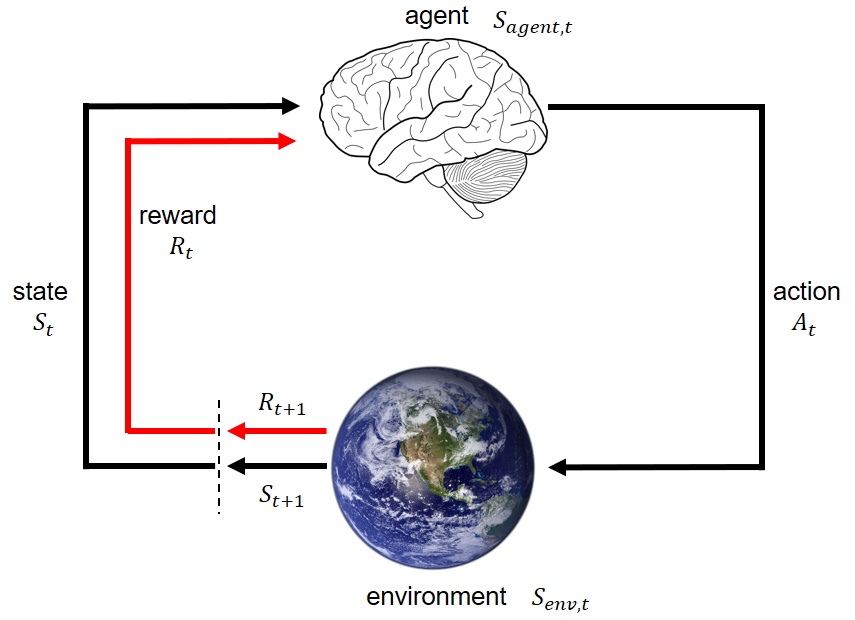
 In the previous post,I gave a high-level overview of Reinforcement Learning (RL). In this post, I will summarize different learning paradigms of RL agents. (more…)
In the previous post,I gave a high-level overview of Reinforcement Learning (RL). In this post, I will summarize different learning paradigms of RL agents. (more…)
Posts in the DataScience category:
Reinforcement learning (I): overview

In the past 2 years, I have been following progress in Reinforcement Learning (RL). RL beats human experts in Go [1], and achieves professional levels in Dota2 [2] and StarCraft [3]. RL is being mentioned more and more often in mainstream media and conferences.
I think it is a good time for me to revisit RL. (more…)
My favorite talks at ICML 2019

Last month, I went to Long Beach, California to attend the 36th international conference machine learning (ICML). Having been to several academic conferences during graduate school in neuroscience (SfN) and biophysics (BPS), I was very excited to go to a comprehensive machine learning conference for the first time. Here are my key takeaways and favorite talks at ICML 2019.
How exactly does Bayesian Optimization work?
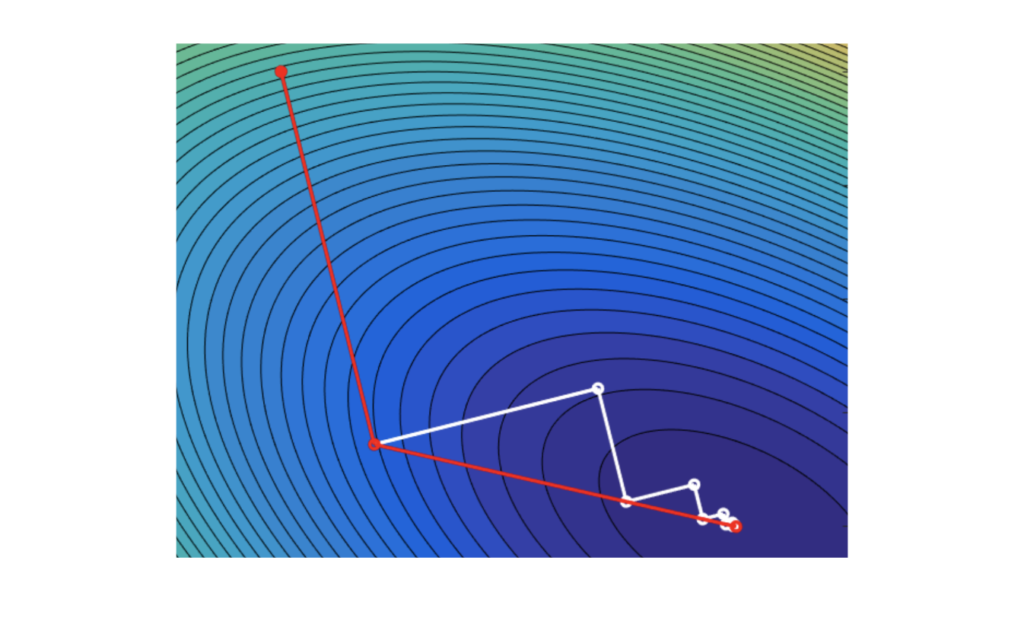
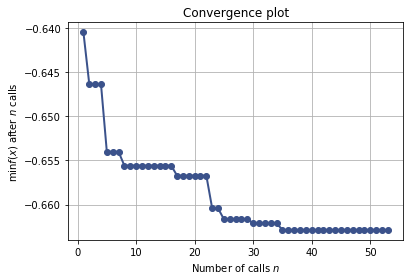
In the previous post, I introduced Bayesian Optimization for black-box function optimization such as hyperparameter tuning. It is now time to look under the hood and understand how the magic happens.
Learn to learn: Hyperparameter Tuning and Bayesian Optimization
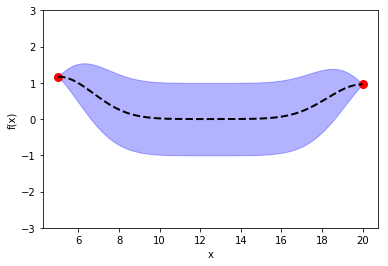
In machine learning models, we often need to manually set various hyperparameters such as the number of trees in random forest and learning rate in neural network. In traditional optimization problems, we can rely on gradient-based approaches to compute optimum. However, hyperparameter tuning is a black box problem and we usually do not have an expression for the objective function and we do not know its gradient. In this post, I will discuss different approaches for hyperparameter tuning and how we can learn to learn.
Numerical optimization in machine learning (III): Constrained optimization
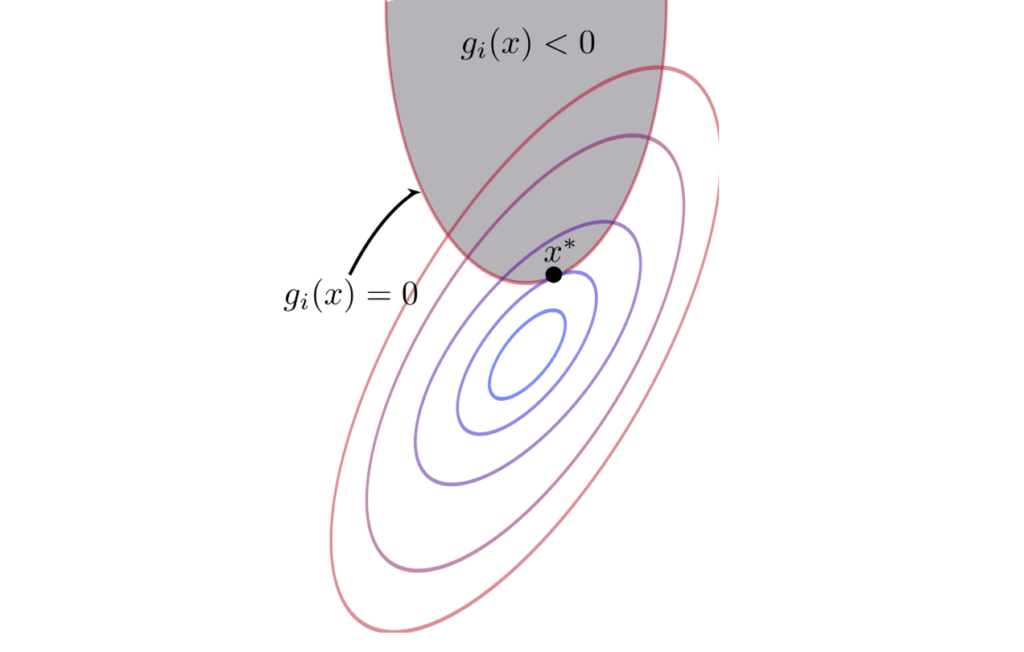
Now what we have discussed unconstrained optimization problems in previous post, it is now time to come to the reality. In the real world, we often have limitations, such as the total budget, motion angles, and some arbitrary desirable range of values. Life would be so easy (and boring) without boundary and conditions. Adding constraints certainly makes optimization problems less easy, but more interesting.
Everything you need to know about matrix in machine learning (II): eigendecomposition and singular value decomposition
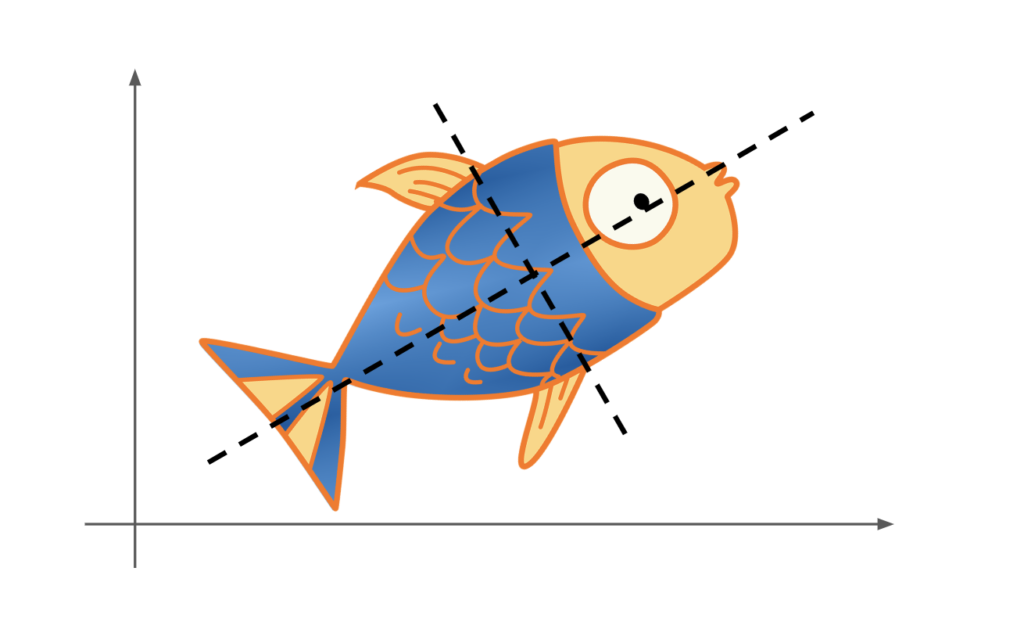
Why do we care about eigenvalues, eigenvectors, and singular values? Intuitively, what do they tell us about a matrix? When I first studied eigenvalues in college, I regarded it as yet another theoretical math trick that is hardly applicable to my life. Once I passed the final exam, I shelved all my eigen-knowledge to a corner in my memory. Years have passed, and I gradually realize the importance and brilliance of eigenvalues, particularly in the realm of machine learning. In this post, I will discuss how and why we perform eigendecomposition and singular value decomposition in machine learning.