In my previous post, I presented interesting trips patterns of NYC taxis. Here, I focus my analysis of Brooklyn. Brooklyn is a very popular place of interest for both tourists and local people to eat, drink, and have fun. I usually take subway train L or G to visit Brooklyn. However, L train is to be shut down in 2019 for 1.5 years [1], which may severely affect Brooklyn’s business. Taxi trips, in particular, shared taxi trips, may become the mainstream transportation in Brooklyn.
To understand possible shared trip, I grouped pickup and dropoff locations by zipcode, neighborhood, and county. In order to do this, I first converted coordinates to address using Geocoder API for green taxi. Since the API is slow, I used single days (Wednesday, Saturday, Sunday) to represent weekday and weekends. I also included Uber data in this analysis, which include the pickup neighborhood information. Check my first post of data wrangling here.
Table of Contents
Trip within Brooklyn
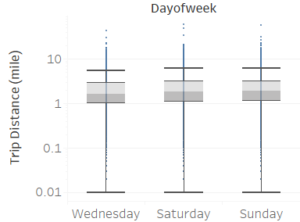
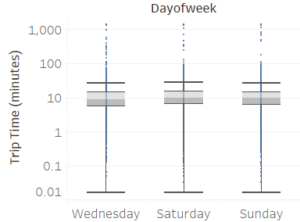
I first looked at trips starting and ending within Brooklyn. Such trips are defined as local trip and they usually have short distances of 2 miles and travel time 10 minutes.
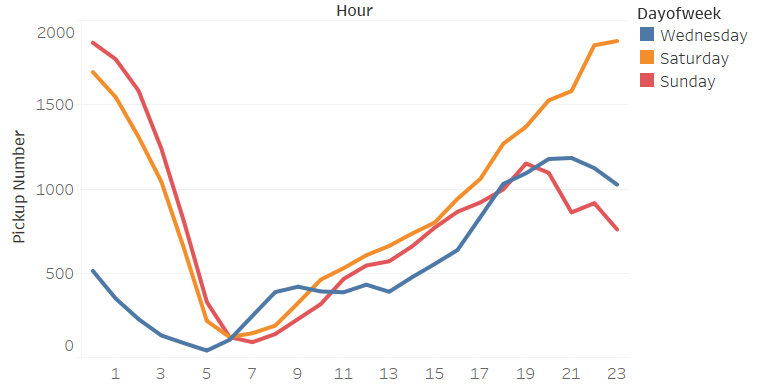
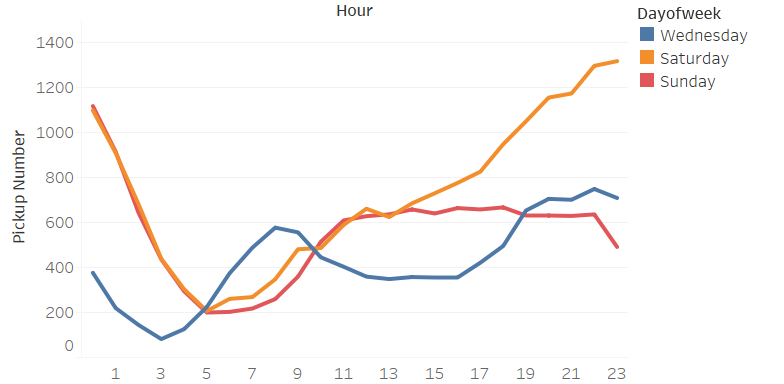
Weekday (Wednesday) pickup in Brooklyn peaked at 9 pm. Saturday pickup peaked at midnight, starting to increase in late afternoon, and lasted to Sunday morning. Sunday however, had a lower pickup late night (lower than Wednesday).
Where did taxi pick up and drop off passengers?
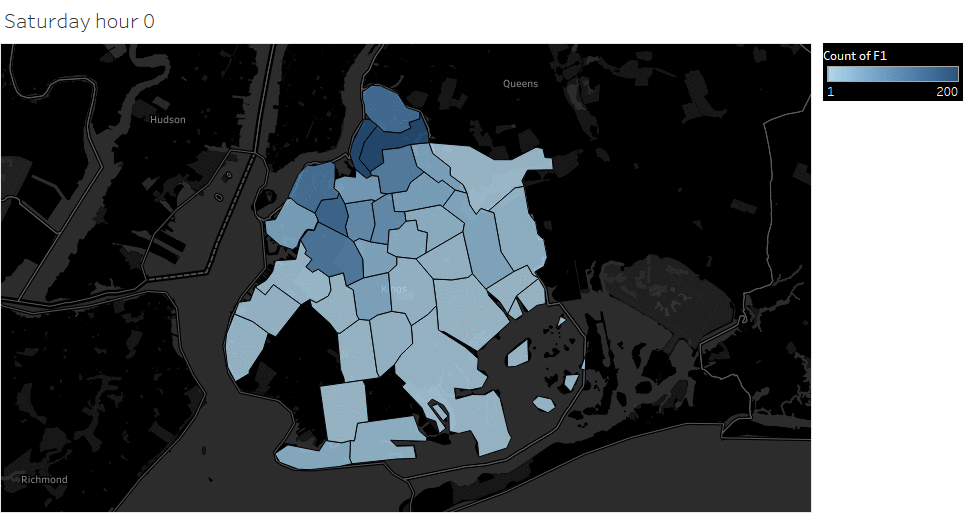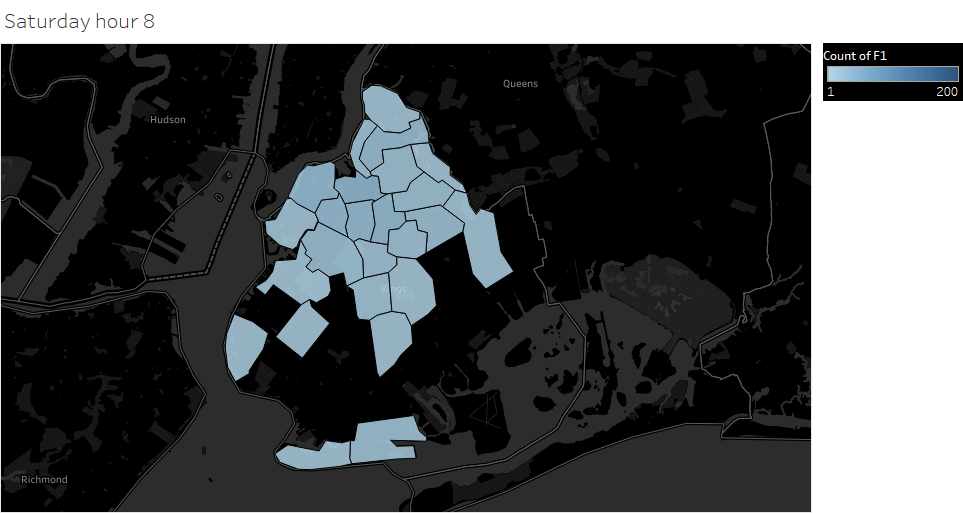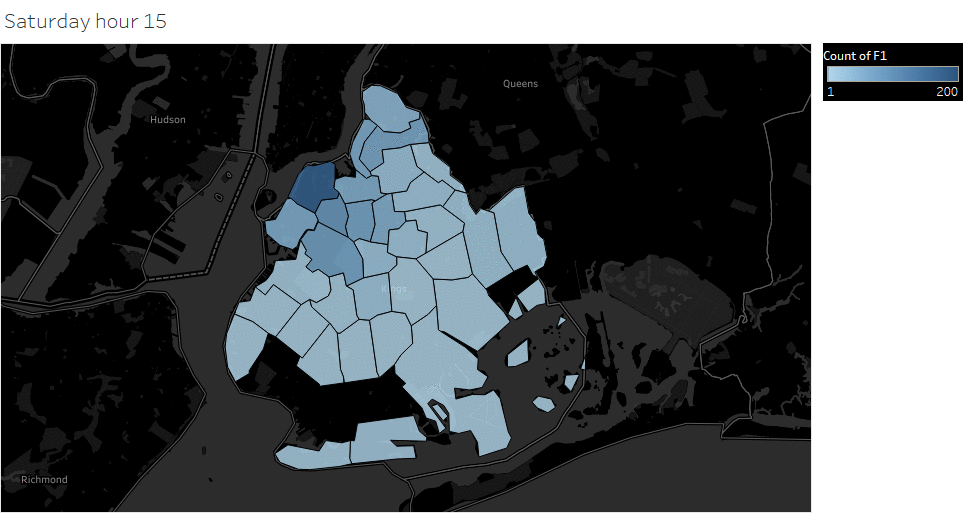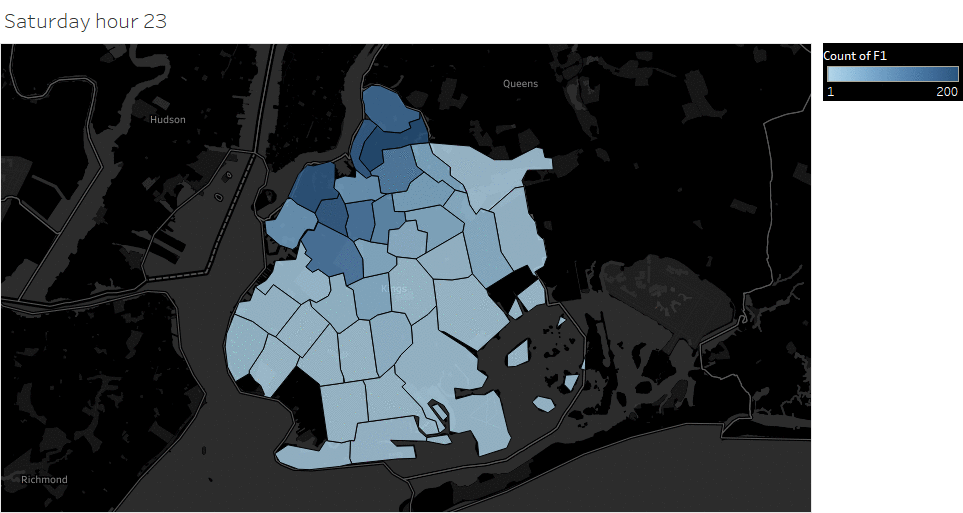
Animated pickup map by hour
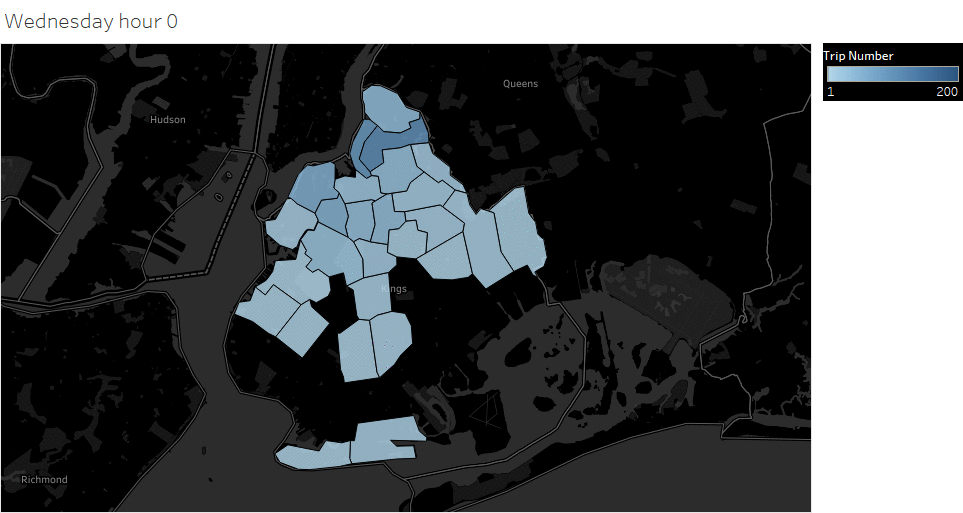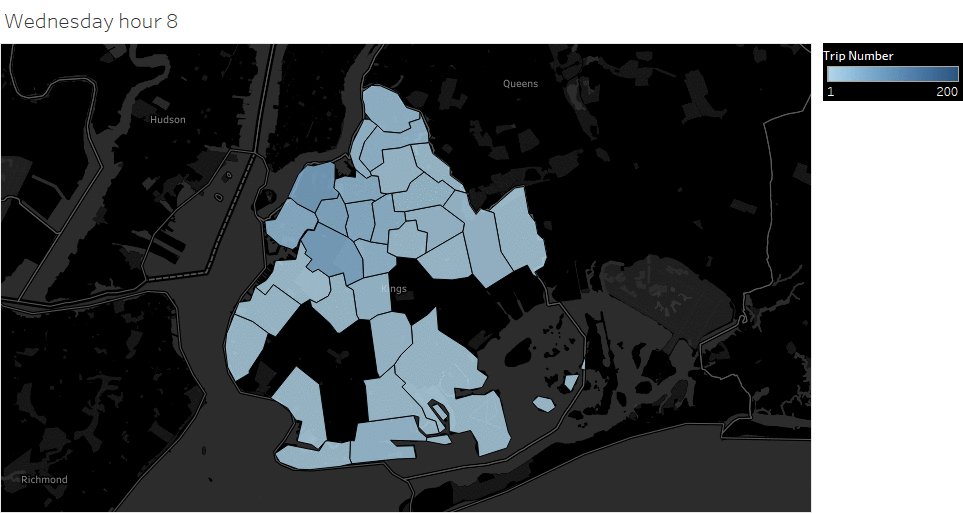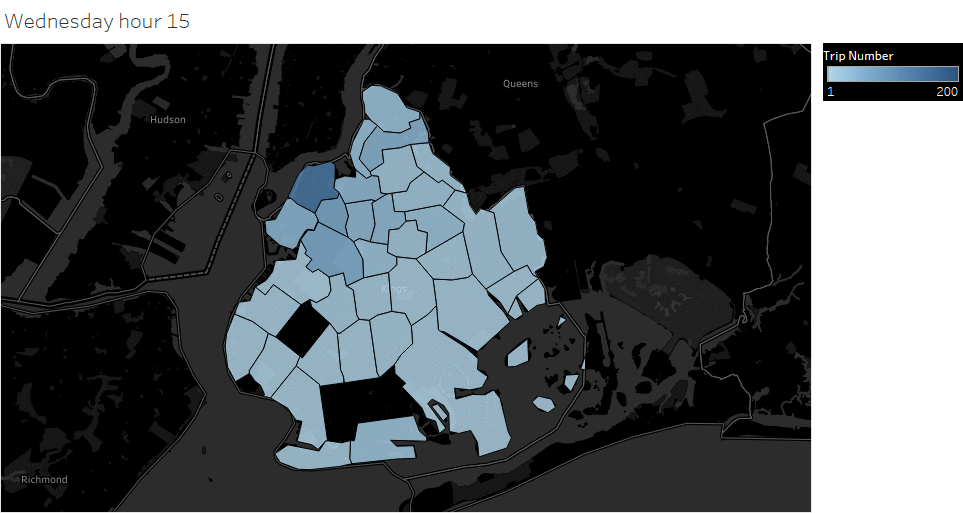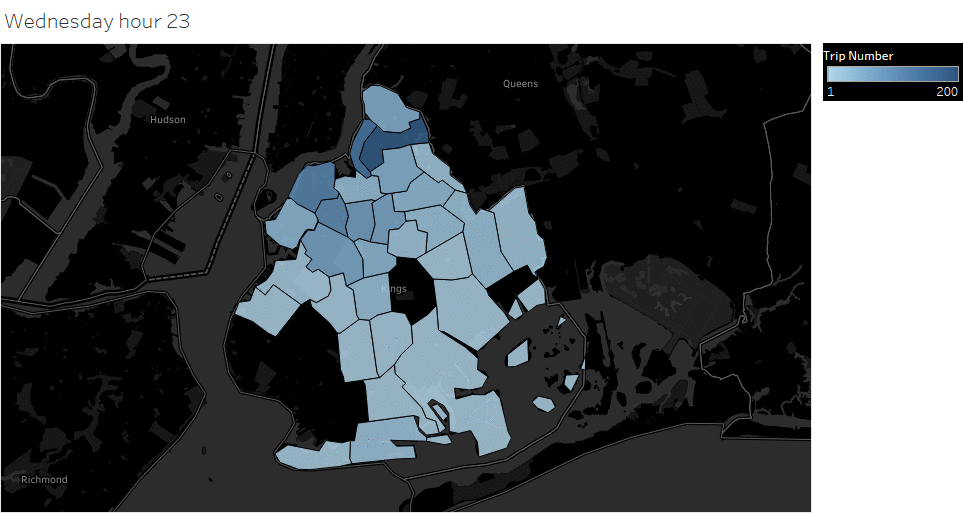
Saturday Pickup in Brooklyn
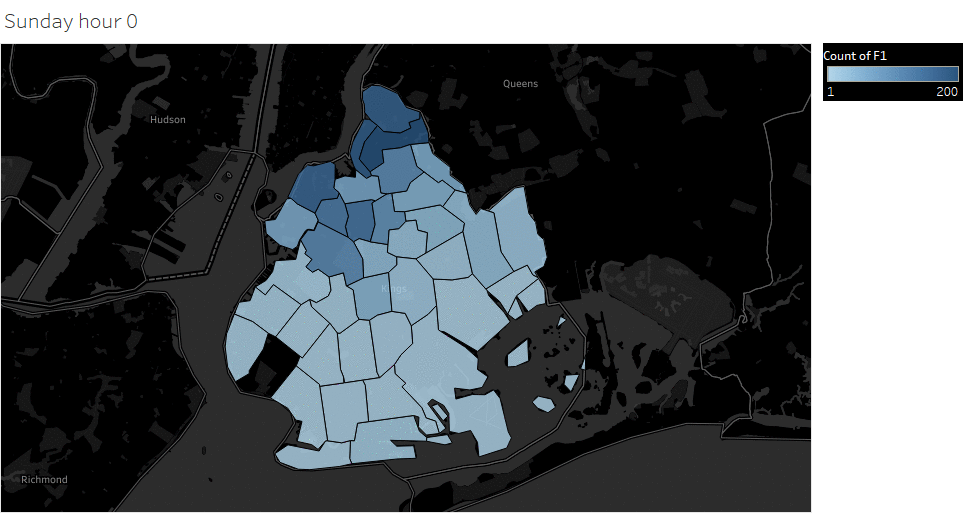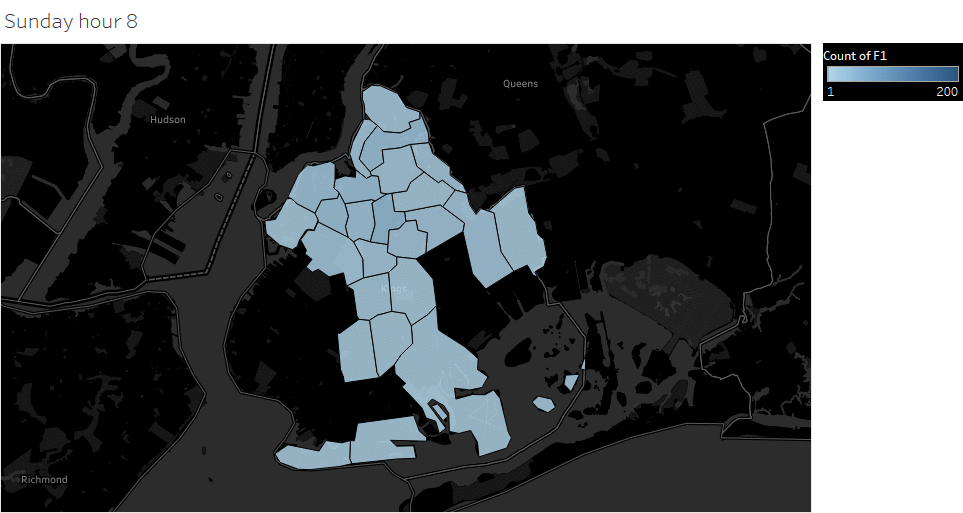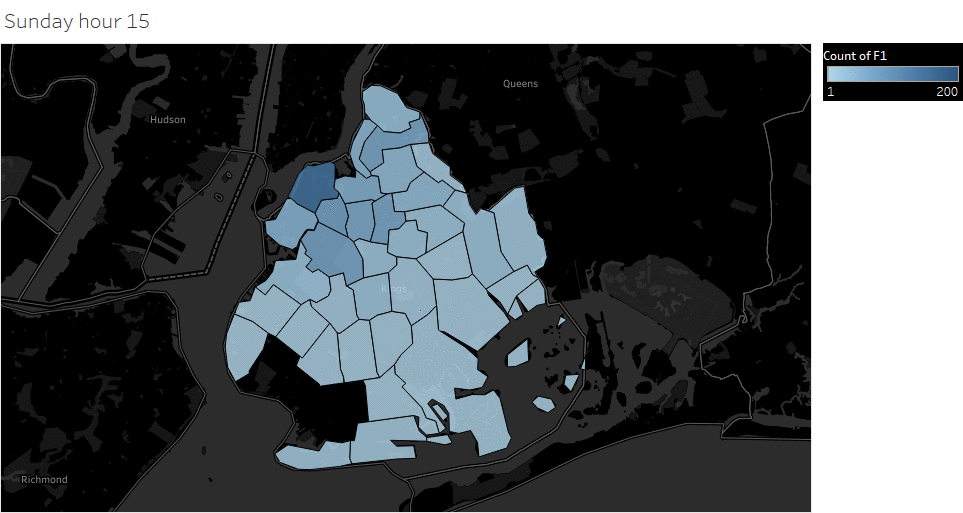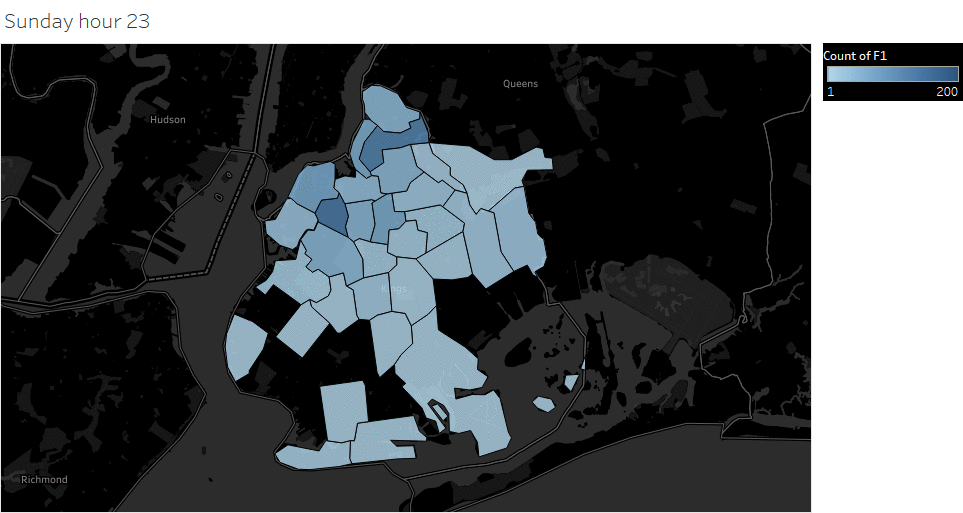
The spatial temporal pattern revealed that evening and late weekend night were the busiest time for certain Brooklyn areas.
Top 10 zip codes for pickups are 11231, 11205, 11216, 11222, 11238, 11215, 11249, 11217, 11211, 11201
Top 10 zip codes for drop off are 11201, 11211, 11217, 11249, 11215, 11238, 11222, 11216, 11205, 11231
Top Neighborhoods
(image url https://en.wikipedia.org/wiki/File:Brooklyn_neighborhoods_map.png)
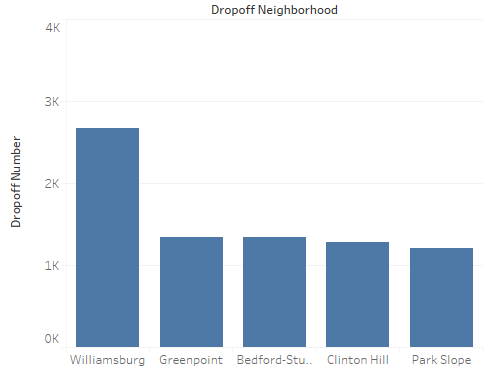
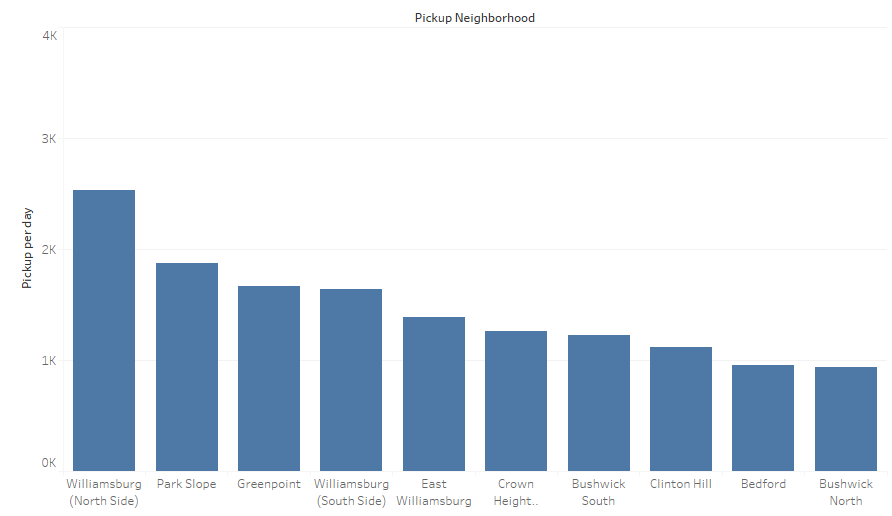
When I grouped trips by neighborhood names, the popular spots became familiar. Williamsburg, Greenpoint, Park Slope, Clinton Hill were hot pickup and drop off spots. In particular, Williamsburg led the 2nd popular spot by 100%.
Uber is also popular in these neighborhoods
I looked at Uber’s pick up records on the same days.
Similar to Green Taxi, Uber trip in Brooklyn also had a morning peak and a evening peak on Weekday. Yet trips droped in the middle of the day. On Saturday (Friday) overnight and Sunday overnight, there were more trips, similar as Green taxi.
Top neighborhoods of Uber, again, include Williamsburg, Park Slope, Greenpoint.
Popular Routes
Now that we know most trips start and end at similar hot spots, I then investigated popular routes in Brooklyn. If some routes are very popular, it may be possible to redesign bus/shuttle routes. Also, if passengers share the same routes, they may also share taxi rides, which only only help passengers to save money, but also increase the efficiency of taxi rides.
I started with Green taxi Saturday data and grouped trips by pickup and dropoff zip codes.
sat_route_zipcode = sat_bk_bk.groupby(['pickup_zipcode','dropoff_zipcode'],as_index=False).count()[['pickup_zipcode','dropoff_zipcode','pickup_datetime']]
sat_bk_bk_distance = sat_bk_bk.groupby(['pickup_zipcode','dropoff_zipcode'],as_index=False).mean()[['pickup_zipcode','dropoff_zipcode','trip_distance']]
sat_routes = sat_route_zipcode.merge(sat_bk_bk_distance)
sat_routes.sort_values('pickup_datetime',ascending=False,inplace=True)
sat_routes.rename(columns = {'pickup_datetime':'trip number'}, inplace=True)
sat_routes
pickup_zipcode dropoff_zipcode trip number trip_distance 1 11201 11201 542 0.989410 254 11211 11211 523 0.934589 265 11211 11222 517 1.243926 937 11249 11211 415 1.054024 540 11222 11211 353 1.300425 249 11211 11206 326 1.619724 948 11249 11222 326 1.163926 29 11201 11231 322 1.530280 16 11201 11217 320 1.289594 352 11215 11215 316 1.091582 279 11211 11249 286 1.002483 423 11217 11215 248 1.354758 962 11249 11249 234 0.743547 410 11217 11201 223 1.339327 4 11201 11205 221 1.522489 14 11201 11215 212 2.279104 354 11215 11217 197 1.170964 549 11222 11222 196 0.937908 264 11211 11221 194 2.662938 36 11201 11238 192 2.123646 563 11222 11249 187 1.270321 445 11217 11238 178 1.214775 932 11249 11206 176 2.181420 719 11231 11231 166 1.214699 10 11201 11211 165 3.591879 694 11231 11201 160 1.537688 246 11211 11201 156 3.810256 107 11206 11211 153 1.360523 425 11217 11217 144 0.840000 64 11205 11201 142 1.552254 ... ... ... ... ... 486 11220 11214 1 3.120000 485 11220 11211 1 9.320000 482 11220 11205 1 8.690000 480 11220 11201 1 4.920000 478 11219 11230 1 3.300000 476 11219 11218 1 4.300000 554 11222 11228 1 11.690000 566 11223 11214 1 1.100000 625 11225 11234 1 4.030000 567 11223 11219 1 1.930000 618 11225 11224 1 2.050000 615 11225 11220 1 4.470000 606 11225 11209 1 7.450000 599 11224 11239 1 9.500000 597 11224 11236 1 8.080000 592 11224 11230 1 4.020000 585 11224 11221 1 3.430000 584 11224 11220 1 5.740000 582 11224 11212 1 10.200000 581 11224 11211 1 15.680000 580 11224 11210 1 6.100000 578 11224 11207 1 10.640000 577 11224 11205 1 15.100000 576 11224 11204 1 4.090000 575 11224 11201 1 12.580000 573 11223 11232 1 8.400000 572 11223 11230 1 2.050000 570 11223 11228 1 3.870000 569 11223 11226 1 4.350000 976 11417 11212 1 1.600000
From the list of popular routes above, I noticed that these trips had same or similar pick up and drop off zip codes, and short trip distance < 2 miles.
I defined shareable trips as trips with pickup time within 5 minutes and with same pickup and dropoff zipcodes. If there are more than 1 trip, number of shareable trips = total passenger number / 6, while 6 is the capability of each taxi. Otherwise, the number of non-shareable trip is 1, for each route and time window. Then for each pickup zipcode, I count the total number of shareable trips and non-shareable trips. Shared ride efficiency for each zipcode = #shareable trips / (#shareable+#non-shareable trips). Hourly ride efficiency is calculated as the mean efficiency across all zip codes.
1 Group by pickup and dropoff zipcode (namely route), and count total trip number, total passenger number, aggr trip number, and non aggr trip number. If total trip number of a certain route is 1, aggr is 0. Otherwise, divided the total number of passengers by 6 given that 6 is the capacity of a taxi. Non aggr trip is 0 when there is aggr trip, otherwise, it is 1.
def aggr_trip(df):
df_gp = df.groupby(['pickup_zipcode','dropoff_zipcode'],as_index=False)
df_trip_num = df_gp.count()[['pickup_zipcode','dropoff_zipcode','pickup_datetime']]
df_passenger_num = df_gp.sum()[['pickup_zipcode','dropoff_zipcode','passenger_count']]
df_eff = df_trip_num.merge(df_passenger_num)
df_eff.rename(columns = {'pickup_datetime':'trip number'}, inplace=True)
df_eff['aggr trip number'] = np.where(df_eff['trip number'] == 1,0,np.ceil(1.*df_eff['passenger_count']/6))
df_eff['non aggr trip number'] = np.where(df_eff['trip number'] == 1,1,0)
return df_eff
2.Calculate shared ride percentage across all areas
def aggr_eff(df):
df_eff = aggr_trip(df)
df2 = df_eff.groupby('pickup_zipcode',as_index=False).sum()[['pickup_zipcode','passenger_count','aggr trip number','non aggr trip number']]
df2['aggr eff'] = 1.*df2['aggr trip number'] / (df2['aggr trip number'] + df2['non aggr trip number'] )
return df2
3 Average across all routes
def aggr_eff_all(df):
if df.empty:
return 0
else:
df2 = aggr_eff(df)
return df2['aggr eff'].mean()
4. ..
Overall, I defined hourly shared ride efficiency.

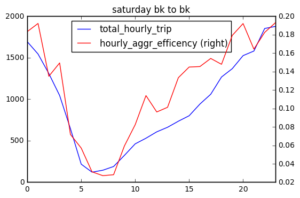
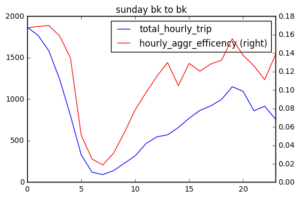
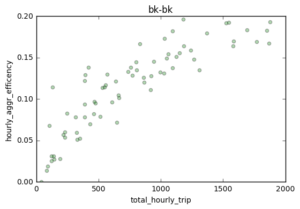
From my calculation, I reported that over 15% of trips on Saturday after 4 pm to Sunday 4 am are shareable. Over 10% of trips on Wednesday morning during rush hour are shareable.
Using similar analysis used above, I also analyzed trips between Brooklyn and Manhattan.
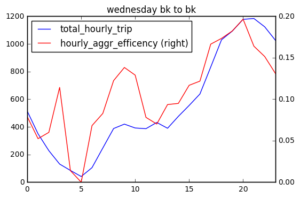
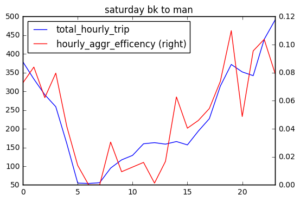
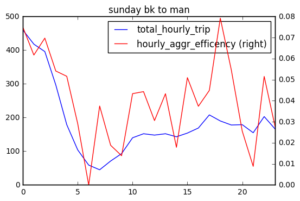
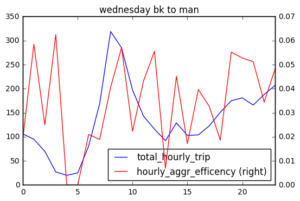
Total Hourly Trip and Shared ride efficiency
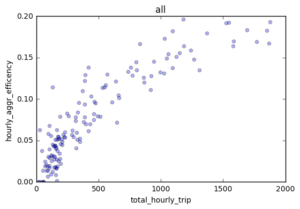
From my definition and calculation of hourly shared ride efficiency, it seems that shared ride efficiency should be correlated to total number of trips. The more trips there are, the more likely shared routes exist.
I plotted hourly shared ride efficiency and total hourly trip number of each day, and find that in general, share ride efficiency changes as total hourly trip number changes. There are several peaks in hourly share ride efficiency (red). Sat 1 am, 2 am, 8 pm; Sun 1-2 am (prolonged peak at midnight) ; Wednesday 3 am and 9 am. These peaks may suggest that at certain time, passengers are more likely go to similar direction.
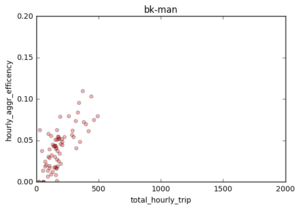
There are fewer trips from Brooklyn to Manhattan compared with trips within Brooklyn and the shared ride efficiency is quite low on Wednesday. On weekend, shared ride efficiency is above 0.06 only after 7 pm Sat to early Sunday. There is a peak on Sunday afternoon to Manhattan.
Linear Correlated?
To understand the correlation between total hourly trip and hourly shared efficiency, I first calculated the pearson correlation coefficient from 3 days (sat,sun,wed), 2 direcition (bk-bk, bk-man), and reported 0.899934, suggesting they are quite highly correlated. Again we can see there are fewer number of Brooklyn to Manhattan trips.
From the above analysis, I realize hourly shared ride efficiency is related to day of the week, hour of the day, destination (bk or man), as well as the total hourly trip. I then built a linear regression model to fit the data and try to predict a hourly shared ride efficiency of any given time.
def add_field(df,col1,col2):
df['to'] = col1
df['day'] = col2
# use numerical data to encode date and destination
add_field(sat_bk_bk_df,0,1)
add_field(sun_bk_bk_df,0,2)
add_field(wed_bk_bk_df,0,3)
add_field(sat_bk_man_df,1,1)
add_field(sun_bk_man_df,1,2)
add_field(wed_bk_man_df,1,3)
Sample size: 144 ( 3 days, 24 hour a day, 2 destination)
Features are ‘hour’, ‘to’, ‘day’
The label is ‘hourly_aggr_efficiency’
| hourly_aggr_efficiency | total_hourly_trip | hour | to | day | |
|---|---|---|---|---|---|
| 0 | 0.183372 | 1694 | 0 | 0 | 1 |
| 1 | 0.192233 | 1545 | 1 | 0 | 1 |
| 2 | 0.134911 | 1310 | 2 | 0 | 1 |
| 3 | 0.149407 | 1045 | 3 | 0 | 1 |
| … | … | … | … | … | … |
from sklearn.cross_validation import train_test_split X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3, random_state=42) reg = linear_model.LinearRegression() reg.fit(X_train,y_train)
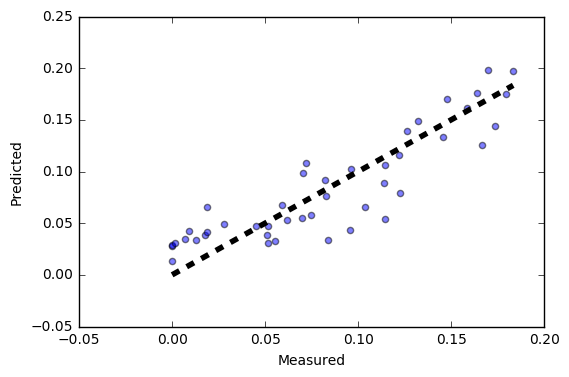
Using reg.score(X_test,y_test), I reported 0.82 R^2 score, suggesting a good fit of the data.
y_pred = cross_val_predict(reg, X_test, y_test,cv=5)
fig, ax = plt.subplots()
ax.scatter(y_test, y_pred,alpha=0.5)
ax.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=4)
ax.set_xlabel('Measured')
ax.set_ylabel('Predicted')
plt.show()
Last but not the least, I used cross validation to show the comparison of predicted value v.s. actual test value. As we can see, at lower shared ride efficiency, the predicted value seems to overestimate while as shared ride efficiency increase, the model seems to underestimate the value. Overall, the regression model provides us a rough idea about the shareability of Broolyn Trips.
References:
[1] L train service between Brooklyn and Manhattan to be shut down for 18 months starting in 2019, http://www.nydailynews.com/new-york/train-shut-18-months-starting-2019-article-1.2725118